Introducing Structured Transparency

Part 1 of my summary of the Private AI series was all about information flows and how they are fundamental to our society. We also learned about how information flows are often broken today because of the privacy-transparency trade-off.

In Part 2, we discussed which technical problems exactly are underlying the privacy-transparency trade-off.

In Part 3, covering the first half of lesson 4, we now learn about solutions.

The course introduces the concept of structured transparency. It aims to provide you with a structured approach to analyze privacy issues. Enable transparency without the risk of misuse.

Examples:

Secret voting is a form of structured transparency. Citizens can express their preferences without having to fear repression.
A sniffer dog. It detects whether a piece of luggage is safe, without revealing the private content.
Another current example that uses technology to allow structured transparency is arms control. Controlling nuclear warheads is very challenging. How to prove the authenticity of a warhead without revealing details about its construction? There is an ingenious method based on physics that allows just this.

Why is structured transparency important now?

There has never been a more important time and need for structured transparency. Digital technology allows collecting and analzying sensitive data at an unprecedented scale. This introduces huge threats to privacy and social stability.
There has never been a more promising time for structured transparency. Recent developments in privacy-enhancing technologies allow high levels of structured transparency that had been impossible earlier. These technologies are improving rapidly and they are pushing the pareto frontier of the privacy-transparency trade-off.

The 5 Components of Structured Transparency

There is a large number of complex privacy technologies available. The structured transparency framework exists to help you break down an information flow into its individual challenges. Then we can figure out which technology is applicable. Structured transparency has the goal to make privacy-enhancing technologies accessible. It wants to build a bridge between technical and non-technical communities.

You should focus on the goals of structured transparency instead of single tools or technologies, because these are always changing and evolving.

The guarantees of structured transparency operate over a flow of information.

The guarantees:

Input privacy
Output privacy
Input verification
Output verification
Flow governance

Input privacy and verification are guarantees about the inputs of an information flow.
Output privacy and verification are guarantees about the outputs of an information flow.
Input and output privacy relate to information that needs to be hidden. Input and output verification refers to information that needs to be revealed in a verifiable way.
Flow governance is concerned with who is allowed to change the flow. This includes who is able to change the input and output privacy and verification guarantees.

Input Privacy

Example: You write a letter to a friend, put it in an envelope, and give it to the postal service. The postal service then uses its knowledge and logistics to navigate the letter to the destination. All without reading your letter, thanks to the envelope. Input privacy in this case means the guarantee that the mailman won't be able to see your inputs (the contents of your letter) to your information flow.

Note: Input privacy is a guarantee that one or more people can participate in a computation, in such a way that neither party learns anything about the other party’s inputs to the computation.

Let's consider a special case that is a bit surprising. What if you sent a letter to the mailman's mother, who reads it out loud to him? This would not violate input privacy, because the information flow had been completed at the moment he delivered the mail.

Important: Input privacy’s guarantee only protects the inputs to an information flow and the intermediate variables within an information flow, but not the outputs.

Consider an information flow like a system of pipes, moving colored water from two inputs into one output. Colored water represents private data. Input privacy guarantees that

the pipes don't leak
information only flows one way.

This means that no person can see which color the other person pours into their pipe.

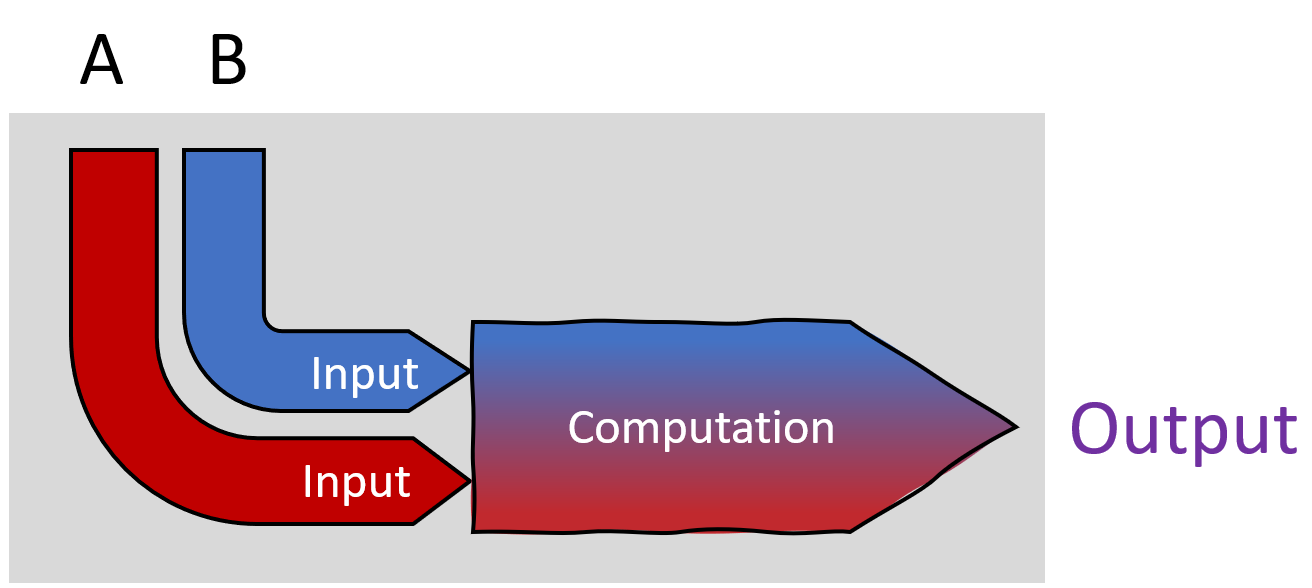
A and B can't know which color the other person pours in.

One exception: If B was connected to the output of the information flow, then they could tell by the color of the output water that someone is feeding in red water. Reverse-engineering inputs from the outputs like this is not violating input privacy. In the graphic, the grey area marks the elements of the information flow that input privacy protects.

There are non-technical solutions to input privacy. A common example is a non-disclosure agreement.

When you make sure that input privacy is satisfied, you can prevent the copy problem. Because it's impossible to copy input information you never see!

Technical Tools for Input Privacy

What's exciting about input privacy is not the guarantee itself, but the new technologies behind it. Recently proposed techniques are providing input privacy in ways that were impossible only a few years ago.

Tool 1: Public-key Cryptography

You use public-key cryptography (PKC) every day, for example while visiting this website 😊 PKC allows to encrypt and decrypt a message using two different keys. We call these the public key and the private key.

Example: You want people to be able to send messages to you. But you want to be sure that no one intercepts these messages. For this purpose, you can use software to generate two keys. A private key that you never share with anyone. And a public key that you can share with everyone. Why can you share the public key with anyone? Because the public key has a special ability: it can encrypt a message in a way that only your private key can decrypt.

Note: In the language of structured transparency, public-key cryptography is a one-way pipe from anyone in the world to you. It doesn’t let anyone else read, change, or process a message on the way to you. This is the simplest form of input privacy.

Notice that this pair of keys is only useful for messages sent to you. If you want to send messages to other people, they need a pair of keys to encrypt messages only they can read. To communicate with a group of people, everyone in the group needs a copy of the public keys of each other.

Tip: Are you using a non-encrypted messenger like Facebook Messenger or Telegram? This is a good time to switch to a secure alternative like Signal! You can compare alternatives here.

Tool 2: Homomorphic Encryption (HE)

Public-key cryptography can create a secure, one-way pipe from anyone in the world to you. However, all this pipe can do is copy information from the input of the pipe to the output of the pipe. While this is very important (for banking systems, the HTTPS protocol for web browsers, etc.), we want to expand this. What if you wanted to perform some kind of computation on this information? This is where encrypted computation comes into play.

Note: Encrypted computation means someone can compute over information, without even knowing the value of the information, because it is encrypted.

Examples: spell-checking a document or translating a document from English to Spanish. Without knowing the contents of the documents!

Before 2009 this was completely impossible. The first algorithm proposing Homomorphic Encryption was too slow for practical purposes. But modern techniques allow running any kind of program over encrypted data. Even intense tasks like sorting algorithms or important machine learning algorithms have become efficient.

Important: If you run a computation on homomorphically encrypted data, the results will always be encrypted with the same key as the input data.

The big generic use case: you can use cloud machines without trusting cloud providers not to look at your data.

Users truly stay in control of their information. In the language of structured transparency: The input privacy guarantee is not only present over the transfer of data, like in a straight pipe. Instead, it also covers all additional transformation or computation steps in the middle of this pipe.

Tip: As a business providing cloud services: with homomorphic encryption, you can guarantee to your customers that you cannot see their data.

This is also useful for storing information. Take your bank as an example: if they stored your information with homomorphic encryption, they would not know how much money you had. But you could still deposit and withdraw as usual.

HE is very general-purpose. Multiple people can take some information, encrypt it with a public key, and then run arbitrary programs on it. The outputs can only be decrypted by whoever has the corresponding private key.

Tool 3: Secure Multi-Party Computation (SMPC)

Note: Secure multi-party computation: Any algorithm wherein multiple people can calculate the outputs of a function, while keeping their inputs secret from each other. It’s a formal group of computational algorithms which satisfy input privacy.

We take a closer look at an interesting one of those algorithms: Additive Secret Sharing. It is very powerful because it allows multiple people to share ownership of a number. This solves the copy problem!

Let's look at an example. I have the number 5 which I want to encrypt. I have two friends, Alex and Bob. I can take the 5 and divide it into two shares, for example, a -1 and a 6. Notice that the sum of these shares still is 5. But the shares themselves contain no information about the encrypted number they represent. We could as well have split it into 582 and -577. The numbers are random, but the relationship between them stores the number 5.

When I give Alex and Bob one of my two shares -1 and 6, neither of them will know which number is encrypted between them. The copy problem no longer applies! Neither Bob nor Alex could copy out the number 5 because they don't know they store the number 5.

With SMPC, no one can decrypt the number alone. All shareholders must agree that the number should be decrypted. It requires a 100% consensus. This is technically enforced shared governance over a number. Not enforced by some law, but by the maths under the hood.

What is even more amazing: while this number is encrypted between Alex and Bob, they can perform calculations on it. Let's double our number. The shares -1 and 6 would be transformed into -2 and 12. The sum of them would be 10, so 5*2✅

The kicker: all programs are numerical operations. At the lowest level every text document, image file or video is just a large number. We could take each individual number and encrypt it across multiple people like Alex and Bob. A file, a program, or an entire operating system could be encrypted this way.

For another example, take a look at this video. There, SMPC is used to calculate the average salary of three employees, and they don't have to reveal their individual salaries.

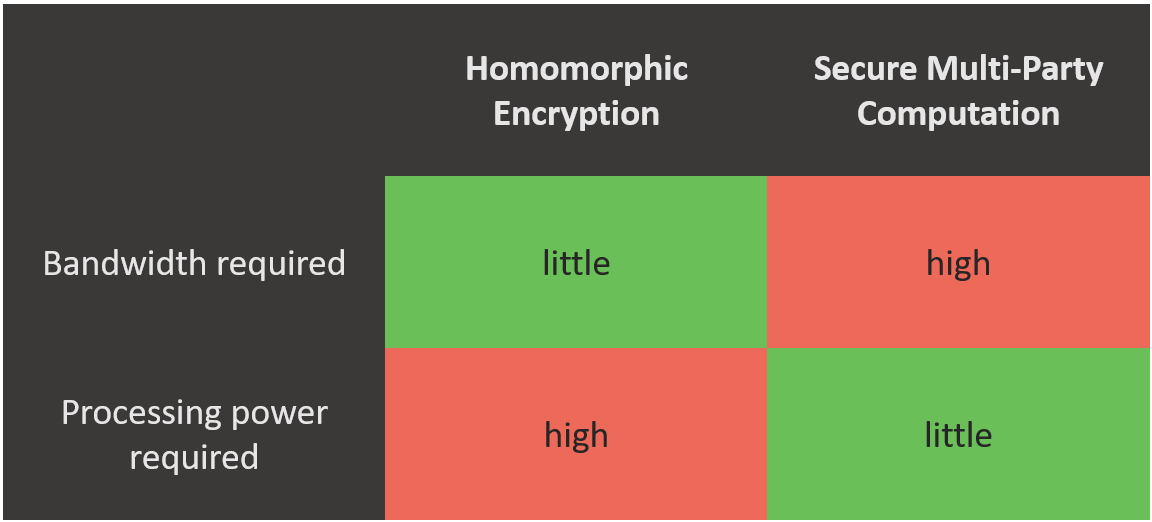
HE and SMPC are only two of many algorithms available for input privacy. Why do we need so many versions? The reason is: different algorithms run faster in different environments. SMPC requires high bandwidth to send the encrypted numbers between devices. But it needs only little computing power. HE on the other hand does not need high bandwidth, but it has to perform a lot of additional steps to perform calculations on encrypted data. So the optimal algorithm depends on your use case.

Output Privacy

Even if an information flow perfectly satisfies input privacy, it can still leak information inside of its contents. While input privacy is mainly concerned with the copy problem, output privacy is mainly concerned with the bundling problem.

Note: Output privacy is about ensuring that certain subsets of information do not make it through the information flow.

If I have an information flow with inputs and outputs, how much can I reverse engineer about the inputs by reading the outputs?

Examples:

If I have the results of the US census, how much could I infer about any particular US citizen by analyzing the census?
When I look at a drug survey, can I infer that an individual participant has a certain disease?

Contents matter! Output privacy is about giving you control over the contents you're sending to people. Unbundle what you want to share from what you don't want to share. The guarantee of output privacy can refer to any fact that can be conveyed in an information flow.

Examples:

While you are on the telephone with your boss, you might want to hide the fact that you are on a beach.
When you participate in a medical study, you might want to stay anonymous, so that your insurance company cannot learn any risk factors of you.
While on a video chat with friends, you might want to blur your background to hide the mess you're in.

And it's not only about the information you are sharing exactly. It's also about information people might use to infer other things about you.

Example: Did you know that analytics companies scrape and parse social media, looking for products and brands in your pictures? You should be able to share what you want to say ("I'm enjoying life on the beach"), without revealing other details. For example, the bottle of medication on the table behind you. Photo post-processing that removes or blurs sensitive items is a great example of output privacy.

Differential Privacy (DP)

Differential privacy is a sophisticated tool for output privacy. It guarantees output privacy in a specific context: aggregate statistics over a large group of people. It tries to unbundle your participation in a survey from a scientist's ability to learn patterns about people who took part in the survey.

To see how Differential Privacy works, let's construct an example. What if Andrew wanted to calculate the average age of all participants of this course. A basic way to do this: everyone sends their age to Andrew. However, this would violate input privacy. Because even though Andrew is only interested in learning the average age (the desired output of the information flow), he'd be learning all the inputs in the process. But we can use input privacy like HE or SMPC to protect everyone's privacy, right? Andrew could calculate the average age without knowing the age of any particular student. It seems that output privacy just happens because input privacy is guaranteed.

But what if Andrew was really clever and sent the survey again to everyone but you. To make the math easy, let's say there are 1,000 students in the course. Previously, the average age was 27. But now, when he runs the survey again without you, the average age is 26.98. Now he could calculate from the difference that you are 20 years old. [Update: originally I said there was an error in the video. This is not the case, see this discussion on GitHub]

Another type of attack: Andrew could also pretend to be the other 999 students. When he gets the final answer, he could subtract the numbers he made up and figure out that you are 47 years old.

Note: When we homomorphically encrypt everyone’s answer, we probably get decent output privacy for free. But we don’t get a true guarantee of output privacy. Because a clever individual running the survey could learn about your personal information.

Differential Privacy can turn such a scenario into a hard guarantee. No one can learn information about you from the average age. How does this work? Instead of sending your age, you first choose a random number between -100 and 100 and add it to your age. So if you're 65 years old and randomly draw the number -70, you'd send Andrew the number -5. So if he reverse-engineered your input using the techniques described above, he'd only learn the number -5 about you.

But doesn't this destroy the accuracy of the average age? Not if we have enough participants. Random numbers have an interesting property. If we randomly choose numbers between -100 and 100, the average of only a few numbers would be very noisy. But the more numbers we look at, the closer to 0 the average moves. If we had infinite numbers, the average would be exactly zero.

Important: If you average over enough random numbers, the randomness cancels out.

So if Andrew averages over enough people in the course, the noise of the random numbers cancels out and he ends up with the same answer. But if it's exactly the same answer, wouldn't the two attacks from before still work?

The first attack: One survey with you included, and another survey with you excluded. Andrew compares the results. Before, the difference between the surveys let him infer your exact age. Now, it is your age plus your random number plus 999 people's random numbers. There is no way of telling your exact age.
The second attack: Andrew pretends to be the other 999 people. Taking the numbers from above, he could only learn -5 about you, which would tell him that you are between 0 and 95 years old - which is true for almost anybody.

Takeaway: Differential Privacy in this example allows Andrew to calculate the average age, without him being able to reverse engineer personal data. In the next section, we discuss DP in a bit more formal way.

Robust Output Privacy Infrastructure

Output privacy is actually a bit more nuanced than we covered before. It's not a binary thing - is output privacy guaranteed or not. This becomes clear when we take another look at our previous example, the average age survey. What if we didn't add numbers between -100 and 100, but between -2 and 2? That would not be great privacy protection. While Andrew wouldn't know your exact age, he would have a pretty good idea.

Output privacy is more like a degree of protection. The more randomness people add to their own data, the better the privacy protection. Differential Privacy lets us measure the difference between a strong privacy guarantee and a weak one. In our example, this is the measure between choosing numbers between -100 and 100, or between -1 and 1. In DP, this measurement is called Epsilon ε.

[Update 25.01.2021] Imagine ε like pixelating an image to hide someone's identity. The more noise we add to the image, the less ε goes out.

Example: A medical research center has data of 3,000 patients. It wants to let outside researchers use their data to cure cancer. How can they make sure that researchers can't reverse engineer their statistical results back to the input medical records? By giving each researcher a privacy budget.

Note: Privacy budget is a measure that says: All your aggregate results that you generate from input data must represent less than X ε of information. X is a measure of maximum tolerance for information reconstruction risk.

When you are not too worried that someone might reconstruct your data, you can set X to 100. If you're really worried, you can set it to 1 or even 0.1. It does not matter which specific algorithm a researcher uses, as long as it can be measured in ε. ε then provides a formal guarantee about the probability that a researcher can reconstruct your private data from their statistical results.
Every researcher gets their own ε. Say you had 10 researchers studying your patients. If every researcher had 20 ε, could they team up and leak up to 200 ε? In theory, they could do so if they combined their results in the right way. If you are sharing data very publicly, you should consider assigning a global ε for all researchers. If you are working with selected researchers unlikely to share information, an individual privacy budget is fine.
Think from the perspective of a patient. How does ε apply to you? Say you are at 2 hospitals and both of them share data with researchers. When both hospitals share 20 ε worth of information about you, that means that in total 40 ε could be leaked! Just because your hospital thinks they are not leaking private information about you, doesn't mean they are not.

Example: Netflix ran an ML competition and released a dataset of users and movie ratings. The dataset was anonymized, meaning no usernames or movie titles were present. This seems like good privacy protection - had IMDb not existed. They also keep large lists of users and movie ratings. It turns out, people often rate movies on both platforms at similar points in time. Researchers from the University of Texas showed that they could de-anonymize some of the Netflix data using this approach. In the terms of DP: When Netflix released some ε, there was already an amount ε public from IMDb. Combined, it was enough ε that researchers could run a de-anonymization attack.

The same attacks can be run on much more sensitive data than movie reviews, for example, medical records or your browser history. The amount of ε running around about you measures the probability that someone can reconstruct your private information from an anonymized dataset.

ε is a formal upper bound on the probability that bad things can happen to you if you participate in a statistical study. Statistical study is a very broad term. It includes using everyday products like Chrome, Firefox, or an Apple product. These companies study how people use their products by collecting anonymized usage data. You are protected in all this by DP, measured by some degree of ε.

How much ε can we consider as safe? There is no single correct answer. But we can transform ε into a more useful number called β, where β = e^ε. Let's say you are deciding whether to participate in a medical study. The study guarantees that no more than 2 β are released. What does this mean? Pick any event in your future, whether it's your insurance premiums going up or your partner leaving you. If β is 2, then β guarantees that the new probability of this event, if you participate in the study, is at most 2 times the previous probability.

Differential Privacy is constructed so that it does not care whether the event seems related. The probability that the event will happen, after you participate in the study, is no greater than β times the current probability.

To be continued

This lesson explored the concept of structured transparency. We took a closer look on the first two guarantees of structured transparency: Input privacy and output privacy.

Tip: The biggest changes will not come from just encrypting existing systems. They will come from new opportunities. Ask yourself: What could I never do until now, because sharing my data would be too risky?

In the next summary, we'll cover the remaining guarantees: Input and output verification as well as flow governance.

If you found a paragraph that needs improvement, please let me know! I'm also happy to hear from you if you found this summary helpful! 😊